Consider the following problem: you have two arrays of bytes representing arbitrary precision integers and you need to “return” a byte array representing their addition. The input arrays are both of the same size in bytes, they represent unsigned integers, and they’re in Little Endian. How would you implement it? You must do so in C, btw.
Firstly, a proposition that makes implementation easier:
- A sum of two n bit integers will require at most one extra bit of
precision to represent it
- \(a,b\leq{2^n}-1\implies{a+b\leq{2(2^{n}-1)}}\)
- \(\implies{a+b\leq{2^{n+1}-2}<2^{n+1}-1}\)
- The upper bound (\(2^{n+1} - 1\)) can be stored in n + 1 bits, hence we need at most n + 1 bits to store \(a+b\)
Using that proposition, we can ensure that the output array has a fixed size and therefore may be allocated by the user beforehand (which is only nice because we’re in C). Yay!
For clarity, the function signature for a solution should look like this:
void (*)(byte_t *ret, byte_t *a, byte_t *b, size_t n);
where ret is the byte array to store the result, a and b are the
input arrays and |a|=|b|=n
Naive
The natural method one may think of is a byte-by-byte approach.
#include <stdint.h>
#include <stdlib.h>
typedef uint8_t byte_t;
void add_bytes_naive(byte_t *ret, byte_t *a, byte_t *b, size_t n)
{
byte_t *carry = ret + n;
*carry = 0;
for (size_t i = 0; i < n; ++i)
{
ret[i] = a[i] + b[i] + *carry;
if (UINT8_MAX - a[i] < b[i] || UINT8_MAX - a[i] - *carry < b[i])
*carry = 1;
else
*carry = 0;
}
}
For the uninitiated and, frankly, lame people who don’t know C, here’s an explanation of the function per loop:
- Perform an addition
- Store the result
- Compute if a carry is needed or not
This is the simplest algorithm I could think of, and should be the kind of thing you reach for in those stupid Leetcode questions with arbitrary precision decimal numbers through… linked lists… (the horror… the absurdity…).
Can we do better?
Optimising the hot loop
The hot part of this solution is obviously the loop: it’s where all the actual computation happens. If we optimise the loop, we optimise the algorithm.
Loop unrolling
A classical optimisation for loops is so called unrolling, where some iterations of the loop are inserted directly into the source code. Consider the following loop:
for (int i = 0; i < 5; ++i)
printf("%d\n", i);
A good compiler would see the constant lower and upper bound and optimise that loop by inlining it directly1:
printf("%d\n", 0);
printf("%d\n", 1);
printf("%d\n", 2);
printf("%d\n", 3);
printf("%d\n", 4);
Loop unrolling can increase the performance of an application as it provides the CPU with a clearer set of instructions to pipeline and process, whereas in a loop the CPU has to speculate at any one time whether it will terminate or not (and sometimes messing up that speculation, causing performance loss).
Figuring out the unrolling
How can we unroll the loop for the naive solution? Unlike the nice situation in the previous section with a bounded loop, the solution must loop over the size of the integers given, which is obviously variable. So it isn’t like we can unroll the entire loop: the algorithm has to work for any size we give it. Loop unrolling doesn’t have to unroll the entire loop, however. We could unroll just a couple iterations, and many optimisers do exactly that.
Two at a time
Instead of inspecting one byte per iteration, what if we
inspected two bytes (i.e. unrolled two iterations)? Then the total
number of iterations would be n/2, and we’d be looking at two bytes
at time from each input.
The great part is that two byte integer addition is well defined on
modern day machines, so we could essentially perform the same steps as
in the naive solution, treating the two bytes as a single uint16_t
and replacing UINT8_MAX with UINT16_MAX.
In the previous byte-by-byte solution processing two bytes requires
two additions and two carry checks. In this new method, we’d copy two
bytes into uint16_t’s then perform one addition and one carry check.
Seems like way less work!
Eight at a time
But wait, if we could unroll the loop to do 2 bytes at a time, couldn’t we do, say, 8 bytes at a time? x64 machines can perform unsigned 8 byte adds in a single instruction. They’re purpose built for doing 8 byte operations really really fast, and even the caches are built around 8 byte boundaries. Moving from the old to this new method would translate 8 individual iterations, each with an addition and a carry check, into one 8 byte add and carry check. This certainly sounds optimal and uses the greatest size the CPU can manage.
What if the bytes aren’t sized for 8 bytes?
What if \(n\not\equiv{0}\mod{8}\)? This implies that \(n=8k+r\) where
\(r\in{[1,7]}\). While we can perform a general unroll for the 8k
iterations, how do we deal with the remaining bytes that don’t neatly
fit into a 8 byte integer? Easy: just pad it! We pad the bytes with
exactly 8-r bytes such that it still fits into a word, and doesn’t
affect the overall addition. The carry check would have to be
specialised for the size, however, as the maximum number that could
fit into r bytes is less than that in 8 bytes.
Let’s write some code
From now on, consider a word_t or WORD to be an 8 byte integer.
typedef uint64_t word_t;
#define WORD_SIZE sizeof(word_t)
How do we figure out how many words are in some number of bytes?
const word_t bound = (size / WORD_SIZE) + (size % WORD_SIZE == 0 ? 0 : 1)
If it’s divisible by 8, then we have no need to pad bytes. Otherwise we need one more word to fit the remaining bytes.
Let’s iterate on this bound:
for (word_t i = 0; i < bound; ++i)
{
const word_t index = WORD_SIZE * i;
const word_t _size = MIN(WORD_SIZE, size - index);
const word_t max =
_size == WORD_SIZE ? UINT64_MAX : ((word_t)1LU << _size) - 1;
Here I calculate some necessary constants. These are:
- Where in the byte array the next word exists (index)
- How many bytes remain in the byte array (_size)
- What’s the maximum size of the bytes we will extract (max)
word_t a_i = 0, b_i = 0;
memcpy(&a_i, a + index, _size);
memcpy(&b_i, b + index, _size);
Here I make the words to add by copying the bytes from our individual
byte arrays. Notice how I’m only copying up to _size. In Little
Endian, order of significance is based on index (index 0 least
significant, index n most), so this does the padding of the word
automatically!2
word_t res = a_i + b_i + ret[size];
memcpy(ret + index, &res, _size);
Here we compute the addition and copy it back into the resulting array.
if ((max - a_i) < b_i || (max - a_i - ret[size]) < b_i)
ret[size] = 1;
else
ret[size] = 0;
Finally the carry computation.
Wait this seems like way more stuff
YES, my dear reader, it sure does. It seems like way, way more work just to get the same result as the naive solution. The naive solution takes 11 lines in total, while this solution takes 19! How could this possibly be more performant?
Let’s profile som code.
Profiling code in C
The idea behind profiling is to run a lot of inputs against the algorithm, then measure the resources consumed. Any solution to this problem shouldn’t require any heap usage, so CPU time is the only metric to measure.
For a good sample set, one should have multiple trials of any one input instance, generating a mean and standard deviation on that input. These measures make it very clear when something is off and whether your testing setup needs more tweaking, so it’s a good idea to calculate them. In total you should have \(mn\) data points, where m is the number of unique input instances and n is the number of trials per instance.
So what input should we use? Let’s use powers of 2 for the sizes of the input, with the input data being filled with random bytes generated at runtime. From my own testing, no statistically interesting results occur until we go for really large powers, so I chose the range of \(2^{20}\) to \(2^{29}\). Though it’s severely unlikely you’re ever going to be computing numbers with 8 million bits of precision, this should force the fast CPUs of today to actually expend some noticeable time in computing it. For the number of trials, I chose 10 for no particular reason. Large number of trials would increase the amount of data, but it would take more than a couple of minutes to compute all these trials if I chose higher.
With just a glance at the problem at hand, we can see that the
performance is clearly bounded by size; the larger the input, the
longer the computation will take. With some tissue paper mathematics,
if it takes n seconds to compute \(2^{20}\) byte numbers, then it
should take roughly \(n2^{9}\) seconds to compute \(2^{29}\) byte numbers.
This gives us an hypothesis to see if the measurements are correct.
In C we can use time.h, in particular clock(), to get CPU time.
A rough template of the profiler would be:
clock_t start = clock(), diff;
algorithm(); // perform computation
diff = clock() - start;
long msec = (diff * 1000) / CLOCKS_PER_SEC;
The variable msec is the number of milliseconds the algorithm took
to compute. Note the use of CLOCKS_PER_SEC, such that msec will
be the actual CPU time taken.
The machine I used to get measurements has a 2nd gen i7 (8 cores), 16GB RAM and quite literally nothing else to do; it’s a headless server with no other processes running on it. This should provide clear data with little to obfuscate the results.
Profiling the naive algorithm
| Power of 2 | Arithemtic average (msec) | Standard deviation |
|---|---|---|
| 20 | 4.0 | 0.0 |
| 21 | 8.0 | 0.0 |
| 22 | 17.0 | 0.0 |
| 23 | 34.0 | 0.0 |
| 24 | 68.0 | 0.0 |
| 25 | 137.0 | 0.0 |
| 26 | 274.0 | 0.0 |
| 27 | 549.1 | 0.3 |
| 28 | 1098.7 | 0.46 |
| 29 | 2191.7 | 18.24 |
We see evidence in line with the observation made; one increase in the power of 2 roughly doubled the time it took to compute. For \(2^{20}\) byte long integers, it took 4ms to compute, whereas \(2^{29}\) byte long took ~2191ms to compute, which clearly follows the linear trend as \(4\cdot{2^9}=2048\approx{2194}\).
Note also the high deviation near the top end; I have never been able to get this below 10 on any one run3.
Profiling the optimised algorithm
| Power of 2 | Arithemtic average (msec) | Standard deviation |
|---|---|---|
| 20 | 1.0 | 0.0 |
| 21 | 2.0 | 0.0 |
| 22 | 4.0 | 0.0 |
| 23 | 9.0 | 0.0 |
| 24 | 19.0 | 0.0 |
| 25 | 38.0 | 0.0 |
| 26 | 77.0 | 0.0 |
| 27 | 154.0 | 0.0 |
| 28 | 308.0 | 0.0 |
| 29 | 616.0 | 0.0 |
Firstly: wow! Across the entire board of results we’ve quartered the time taken to perform the same computation, therefore quadrupling the performance. While still following the same overall trend (linear time algorithm), the general speed is much better than the other scheme. Furthermore, notice the nonexistent standard deviation in comparison to the naive algorithm.
Pretty graph
Here’s a graph of powers of 2 against time taken, with error bars for the deviation:
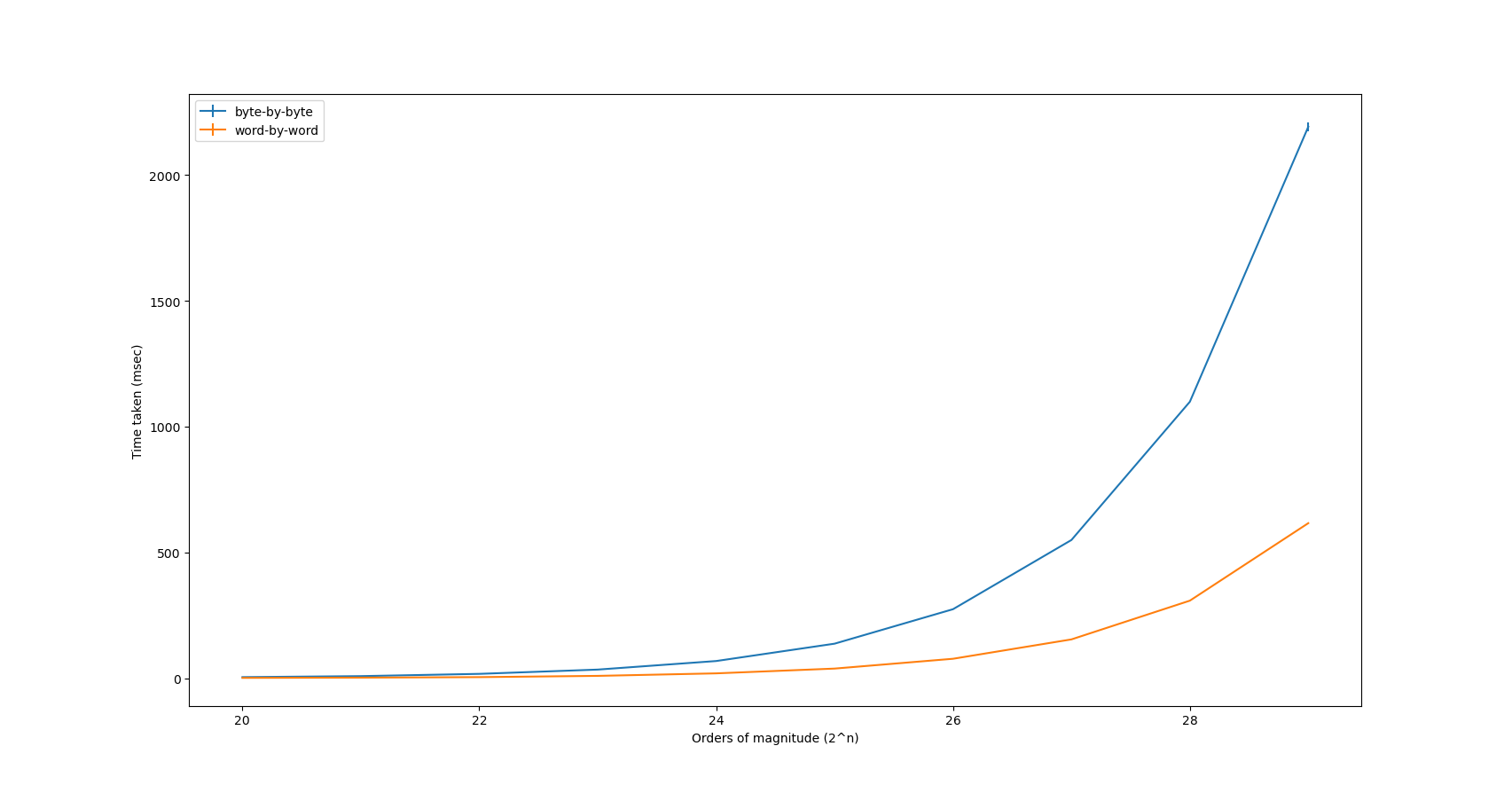
Figure 1: Graph of measurements
It really displays the difference in the two algorithms at scale.
Conclusion
This article and the measurements made are a testament to performance measuring, in particular the fact that one cannot provide any assertions on performance without statistical evidence. Under any number of heuristics the optimised code may be considered “less optimal” than the naive code, but the performance metrics prove that it is indeed the optimal solution.
My next article will be on exploring x86… maybe.
Finally, all the code written (including the profiler) are stored here so go take a look at it.
-
An even better one would just inline the format directly
printf("%d\n%d\n%d\n%d\n%d\n", 0, 1, 2, 3, 4)↩︎ -
NOTE: This assumes a Little Endian host machine. If you’re using Big Endian, you’ll need to swap the input bytes before copying them into a 8 byte integer. Otherwise… pain. ↩︎
-
This may have something to do with the much higher number of cache misses under this algorithm. ↩︎